algo

2020-12-22 约 4660 字预计阅读 10 分钟收录于算法

差分数组

差分数组适用于区间修改问题，如对一个区间内的元素都加1

//差分数组
dif[0] = arr[0]
for (int i = 1; i < n; i++) {
    dif[i] = arr[i] - arr[i-1];
}

//前缀和
for (int i = 1; i <= n; i++) {
    sum[i] = arr[i-1] + sum[i-1];
}

//二维前缀和
for (int i = 1; i <= m; i++) {
    for (int j = 1; j <= n; j++) {
        sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + arr[i][j];
    }
}

lowbit（低位）运算

lowbit(n)定义为非负整数nn在二进制表示下“最低位的1及其后边所有的0”构成的数值

lowbit(n)=n&(∼n+1)=n&(−n)

树状数组

树状数组动态地维护前缀和
常用来求解单点修改和区间查询相关的问题，如求数组左侧或右侧小于(或大于)当前元素的个数，故也可以用来求逆序数问题

//定义树状数组
// 树状数组从下标1开始存
vector<int> arr(n+1,0)

// 向第i(1..n)个位置增加val  log(n)
void add(int i, int val, int n) {
    while (i <= n) {
        arr[i] += val;
        i += i&-i;
    }
}

// 求i位置的前缀和  log(n)
int sum(int i) {
    int res = 0;
    while (i > 0) {
        ret += arr[i];
        i -= i&-i;
    }
    return res;
}

树状数组求逆序对：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
求数组右侧小于当前元素的个数：https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/

数组离散化(压缩)

对数据值不在意，只在意数据之间的相对大小是，可进行数组压缩

vector<int> tmp = nums;
sort(tmp.begin(), tmp.end());
for (int i = 0; i < nums.size(); i++) {
    //当有数据0出现时，由于0&0=0，无法更新，此时我们可以采取加一个数的方法将所有的数据都变成大于0的。若用树状数组则加一，否则不必
    nums[i] = lower_bound(tmp.begin(), tmp.end(), nums[i]) - tmp.begin() + 1;
}
//lower_bound返回数组中第一个大于等于num的元素的迭代器，则lower_bound()-tmp.begin()就是返回元素的下标
//lower_bound之前一定要排序，lower_bound使用二分查找
//若原始数组为[1,3,3,10,100]，则离散化之后的为[1,2,2,4,5]，所以当之后以元素当下标去开数组时，最大就是原数组的大小，即所开数组大小只有原数组长度有关，而与数组中元素的大小无关了，节省了空间

快速幂

V1 不推荐

long long power(long long a, long long b) {
    long long res = 1;
    a %= mod;
    while (b) {
        if (b&1) res = res*a%mod;
        b >>= 1;
        a = a*a%mod;
    }
    return res;
}

V2 推荐

double myPow(double x, int n) {
    if (n == 0) return 1;

    double tmp = myPow(x, n/2);
    if (n % 2 == 0) {
        return tmp*tmp;
    }
    else {
        if (n < 0) return tmp*tmp*(1/x);
        else return tmp*tmp*x;
    }
}

V3 推荐大数取余

long long pow(long long a, long long b) {
    if (b == 0) return 1;

    long long tmp = pow(a, b/2) % mod;
    if (b % 2 == 0) {
        return tmp*tmp % mod;
    }
    else 
      return tmp*tmp*a % mod;
}

逆元

long long inv(long long x) {
    return power(x,mod-2);
}

组合

隔板法

如求方程 x+y+z=10的正整数解的个数：
可将10个球排成一排，球与球之间形成9个空隙，将两个隔板插入这些空隙中（每空至多插一块隔板），规定由隔板分成的左、中、右三部分的球数分别为x、y、z之值，则隔法与解的个数之间建立了一一对立关系，故解的个数可用公式C(n-1,m-1)=C(9,2)=36，也可通过推演得出：将第一个隔板放在第一个间隙，第二个隔板还有8个间隙，若将第一个隔板放在第二个间隙，则第二个隔板还有7个间隙，即8+7+…+1=36

https://blog.csdn.net/sdz20172133/article/details/81431066

C(n,m)求解

long long C(long long n, long long m) {
    long long res = 1;
    for (int i = 1; i <= m; i++) {
        res = res * (n-i+1) % mod;
        res = res*inv(i) % mod;  //inv为逆元
    }
    return res;
}

排序

二分模板

先明确红蓝区域划分，再确定是返回l还是r

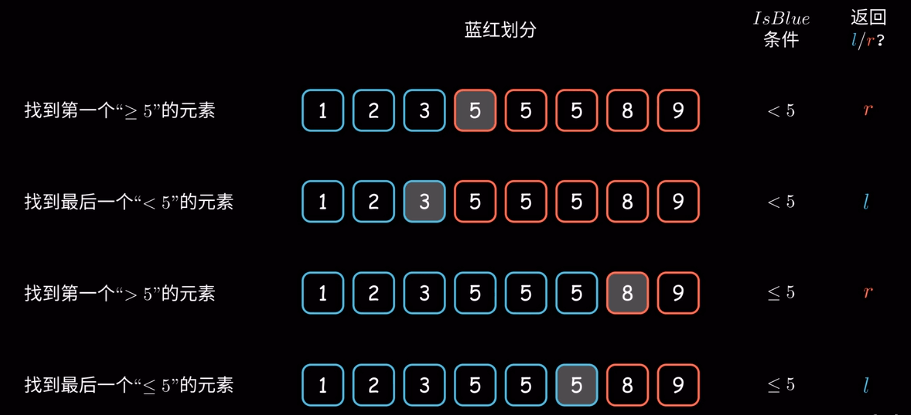
模板只有if判断条件和返回值需要改变
if条件：<是左边界，<=是右边界

//返回target的左边界
int binary_searchL(vector<int>& nums, int target) {
    int l = -1, r = nums.size();
    while (l+1 < r) {
        int mid = l + (r-l)/2;
        if (nums[mid] < target) l = mid;
        else r = mid;
    }
    return r;
}
//返回target的右边界
int binary_searchR(vector<int>& nums, int target) {
    int l = -1, r = nums.size();
    while (l+1 < r) {
        int mid = l + (r-l)/2;
        if (nums[mid] <= target) l = mid;
        else r = mid;
    }
    return l;
}

归并排序

class Solution {
public:
    vector<int> tmp(nums.size());
    void mergeSort(vector<int>& nums, int l, int r) {
        if (l >= r) return;
    
        int mid = l + (r-l)/2;
        mergeSort(nums, l, mid);
        mergeSort(nums, mid + 1, r);
    
        int i = l, j = mid + 1;
        int cnt = 0;
        while (i <= mid && j <= r) {
            //小于等于是稳定的排序，小于是非稳定的
            if (nums[i] <= nums[j]) {
                tmp[cnt ++] = nums[i ++];
            } else {
                tmp[cnt ++] = nums[j ++];
            }
        }
        
        while (i <= mid) tmp[cnt ++] = nums[i ++];
        while (j <= r) tmp[cnt ++] = nums[j ++];
        
        for (int i = l; i <= r; i++) {
            nums[i] = tmp[i-l];
        }
    }

    vector<int> sortArray(vector<int>& nums) {
        tmp.resize((int)nums.size(), 0);
        mergeSort(nums, 0, (int)nums.size() - 1);
        return nums;
    }
};

快速排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        qsort(nums, 0, nums.size()-1);
        return nums;
    }

    void qsort(vector<int>& nums, int l, int r) {
        if (l >= r) return;

        int mid = partition(nums, l, r);
        qsort(nums, l, mid-1);
        qsort(nums, mid+1, r);
    }

    int partition(vector<int>& nums, int l, int r) {
        int pivot = nums[l]; /// 1 保存
        while (l < r) {
                           // 此处一定要大于等于，不能省略等于号；下同
            while (l < r && nums[r] >= pivot) r--;
            nums[l] = nums[r];
            while (l < r && nums[l] <= pivot) l++;
            nums[r] = nums[l];
        }
        nums[l] = pivot;  ///  2  恢复
        return l;
    }
};

堆排序

用数组存储的大顶堆，是一棵完全二叉树

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        heapSort(nums);
        return nums;
    }

    void heapSort(vector<int>& nums) {
        int n = nums.size();
        //建堆，从最后一个结点的父节点开始到结点0，依次做heapfiy。其中第i个结点的父节点为(i-1)/2
        // 注意：n-1-1
        for (int i = (n-1-1)/2; i >= 0; i--) {
            heaify(nums, n, i);
        }

        //排序，交换第一与最后一个结点，然后对第一个结点进行heapfiy，参与heapfiy的数组长度减一
        for (int i = n-1; i >= 0; i--) {
            swap(nums[i], nums[0]);
            heaify(nums, i, 0);
        }
    }

    //递归实现堆调整，对第i个结点从上到下调整
    void heaify(vector<int>& nums, int n, int i) {
        if (i >=n) return;

        int c1 = 2*i+1, c2 = 2*i+2;
        int max = i;
        if (c1 < n && nums[c1] > nums[max]) max = c1;
        if (c2 < n && nums[c2] > nums[max]) max = c2;
        if (i != max) {
            swap(nums[i], nums[max]);
            heaify(nums, n, max);
        }
    }
};

堆的push和pop：

push
1. 添加到数组尾部，然后从下至上比较当前值与其父节点值的大小，如果是大顶堆，则大于父节点则交换，否则停止
pop
1. 交换堆顶与最后一个，然后对堆顶元素进行调

图

Dijkstra

求单源、无负权的最短路

Floyd算法

求多源、无负权的最短路，推荐Floyd，相对于迪杰斯特拉更好记忆

//floyd算法 求最短路径
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        //无穷大初始化为0x3f3f3f3f，原因是两个无穷大相加不会超出范围，并且好记
        vector<vector<int>> cost(n+1, vector<int>(n+1, 0x3f3f3f3f));
        
        //自己到自己的距离为0
        for (int i = 1; i <= n; i++) cost[i][i] = 0;
        
        for (auto& e : times) {
            cost[e[0]][e[1]] = e[2];
        }

        // 遍历每个顶点，当此顶点加入时，是否有经过此节点的最短路径
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    cost[i][j] = min(cost[i][j], cost[i][k]+cost[k][j]);
                }
            }
        }

        int res = 0;
        for (int i = 1; i <= n; i++) {
            res = max(res, cost[k][i]);
        }

        return res >= 0x3f3f3f3f ? -1 : res;
    }
};

BFS求图的相关问题

trie树

struct node {
    node* next[26];
    bool isEnd;
};

node* trie = nullptr;

void insert(string str) {
    if (trie == nullptr) trie = new node();
    node* t = trie;
    
    for (const auto& e : str) {
        if (t->next[e-'a'] == nullptr)
            t->next[e-'a'] = new node();
        t = t->next[e-'a'];
    }
    t->isEnd = true;
}

bool startWith(string prefix) {
    node* t = trie;
    for (const auto& e : prefix) {
        if (t == nullptr) return false;
        if (t->next[e-'a'] == nullptr) return false;
        t = t->next[e-'a'];
    }
    return true;
}

bool search(string word) {
    node* t = trie;
    for (auto& e : word) {
        if (t == nullptr) return false;
        if (t->next[e-'a'] == nullptr) return false;
        t = t->next[e-'a'];
    }
    return t->isEnd;
}

并查集

并查集这三个字，一个字代表一个意思。

并（Union），代表合并
查（Find），代表查找
集（Set），代表这是一个以字典为基础的数据结构，它的基本功能是合并集合中的元素，查找集合中的元素
并查集的典型应用是有关连通分量的问题
并查集解决单个问题（添加，合并，查找）的时间复杂度都是O(1)O(1)。因此，并查集可以应用到在线算法中

并查集跟树有些类似，只不过她跟树是相反的。在树这个数据结构里面，每个节点会记录它的子节点。在并查集里，每个节点会记录它的父节点。
可以看到，如果节点是相互连通的（从一个节点可以到达另一个节点），那么他们在同一棵树里，或者说在同一个集合里，或者说他们的祖先是相同的。

参考链接

class UnionFind{
private:
    // 记录父节点
    unordered_map<int,int> father;
};
//添加节点，当把一个新节点添加到并查集中，它的父节点为其自己
void add(int x){
    if(father.find(x) == father.end()) {
        father[x] = x;
    }
}
//合并节点：如果发现两个节点是连通的，那么就要把他们合并，也就是他们的祖先是相同的。这里究竟把谁当做父节点一般是没有区别的。
void merge(int x,int y){
    int root_x = find(x);
    int root_y = find(y);
    
    if(root_x != root_y){
        father[root_x] = root_y;
    }
}
//判断两节点是否连通
bool is_connected(int x,int y){
    return find(x) == find(y);
}
//查找一个节点的祖先
int find(int x){
    int t = x;
    
    while(father[t] != t){
        t = father[t];
    }
    
    return t;
}
//这里有一个优化的点：如果我们树很深，比如说退化成链表，那么每次查询的效率都会非常低。所以我们要做一下路径压缩。也就是把树的深度固定为二。
int find(int x){
    int t = x;
    
    while(father[t] != t){
        t = father[t];
    }
    
    // 路径压缩
    while(x != t){
        int fa = father[x];
        father[x] = t;
        x = fa;
    }
    
    return t;
}

完整代码

class UnionSet {
public:
    void add(int x) {
        if  (uset.find(x) == uset.end()) {
            uset[x] = t;
        }
    }

    int findRoot(int x) {
        int t = x;

        while (uset[t] != t) {
            t = uset[t];
        }

        while (t != x) {
          int fa = uset[x];
          uset[x] = t;
          x = fa;
        }

        return t;
    }

    bool isConnected(int x, int y) {
        return findRoot(x) == findRoot(y);
    }

    void merge(int x, int y) {
        int xr = findRoot(x);
        int yr = findRoot(y);

        if (xr != yr) {
            uset[xr] = yr;
        }
    }
private:
    unordered_map<int,int> uset;
};

例题:https://leetcode-cn.com/problems/number-of-provinces/

LRU

class LRUCache {
public:
    LRUCache(int capacity) : _capacity(capacity) {

    }
    
    int get(int key) {
        if (mp.find(key) == mp.end()) return -1;
        if (li.front().first == mp[key]->first) return mp[key]->second;

        // auto it = mp[key];
        // int value = it->second;
        // li.erase(it);
        // li.push_front(make_pair(key,value));
        // mp[key] = li.begin();
        li.splice(li.begin(), li, mp[key]);

        // return value;
        return mp[key]->second;
    }
    
    void put(int key, int value) {
        if (mp.find(key) != mp.end()) {
            // li.erase(mp[key]);
            // li.push_front(make_pair(key,value));
            // mp[key] = li.begin();
            li.splice(li.begin(), li, mp[key]);
            li.front().second = value;
        }
        else {
            if (li.size() < _capacity) {
                li.push_front(make_pair(key,value));
                mp[key] = li.begin();
            }
            else {
                auto k = li.back();
                li.pop_back();
                mp.erase(k.first);
                li.push_front(make_pair(key,value));
                mp[key] = li.begin();
            }
        }
    }

    int _capacity;
    list<pair<int,int>> li;
    unordered_map<int,list<pair<int,int>>::iterator> mp;
};

LFU

struct Node {
    int key;
    int val;
    int freq;
};

class LFUCache {
public:
    LFUCache(int capacity) {
        capacity_ = capacity;
        min_freq = 0;
    }
    
    int get(int key) {
        if (key2addr.find(key) == key2addr.end()) return -1;
        auto addr = key2addr[key];
        int ret = addr->val;
        addr->freq++;
        freq2data[addr->freq].splice(freq2data[addr->freq].end(), freq2data[addr->freq-1], addr);
        
        if (min_freq == addr->freq-1 && freq2data[addr->freq-1].size() == 0) min_freq++;

        return ret;
    }
    
    void put(int key, int value) {
        if (key2addr.find(key) != key2addr.end()) {
            auto addr = key2addr[key];
            addr->val = value;
            addr->freq++;
            freq2data[addr->freq].splice(freq2data[addr->freq].end(), freq2data[addr->freq-1], addr);
            if (min_freq == addr->freq-1 && freq2data[addr->freq-1].size() == 0) min_freq++;
        }
        else {
            if (key2addr.size() < capacity_) {
                freq2data[1].push_back({key,value,1});
                auto addr = freq2data[1].end();
                key2addr[key] = --addr;
                min_freq = 1;       
            }
            else if (capacity_ != 0){
                int pre_key = freq2data[min_freq].front().key;
                key2addr.erase(pre_key);
                freq2data[min_freq].pop_front();
                freq2data[1].push_back({key,value,1});
                auto addr = freq2data[1].end();
                key2addr[key] = --addr;
                min_freq = 1;
            }
        }
    }

    unordered_map<int, list<Node>::iterator> key2addr;
    unordered_map<int, list<Node>> freq2data;
    int capacity_;
    int min_freq;
};

位运算

lowbit(n)定义为非负整数nn在二进制表示下“最低位的1及其后边所有的0”构成的数值

lowbit(n)=n&(−n)

将二进制的最后面的1置为0

n = n&(n-1)

方向数组

int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};

动态规划

背包问题

如果求组合数就是外层for循环遍历物品，内层for遍历背包。（若用滚动数组，则01背包的背包遍历需倒序，完全背包的背包正序遍历）
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

背包问题的判定：
给定一个数组，由数组中的元素能否满足所要求的条件
如给定一个target，target可以是数字也可以是字符串，再给定一个数组nums，nums中装的可能是数字，也可能是字符串，问：能否使用nums中的元素做各种排列组合得到target。此问题的背包为target
再如LC474一和零：给你一个二进制字符串数组strs和两个整数m和n。请你找出并返回strs的最大子集的大小，该子集中最多有m个0和n个1。此问题的背包为m和n，故此背包是个二维的

常见的背包问题有1、组合问题。2、True、False问题。3、最大最小问题

组合问题：
1. 组合总和 Ⅳ
2. 目标和
3. 零钱兑换 II
True、False问题：
1. 单词拆分
2. 分割等和子集
最大最小问题：
1. 一和零
2. 零钱兑换

组合问题公式：dp[i] += dp[i-num]
True、False问题公式：dp[i] = dp[i] or dp[i-num]
最大最小问题公式：dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)

当然拿到问题后，需要做到以下几个步骤：
1.分析是否为背包问题。
3.是0-1背包问题还是完全背包问题，也就是题目给的nums数组中的元素是否可以重复使用。
4.如果是组合问题，是否需要考虑元素之间的顺序。需要考虑顺序有顺序的解法，不需要考虑顺序又有对应的解法。

背包问题技巧：

0-1背包
1. 组合：nums放在外循环，target在内循环，且target内循环倒序
2. 排列：将target放在外循环，将nums放在内循环，且target外循环倒序
完全背包
1. 组合：nums放在外循环，target在内循环，且target内循环正序
2. 排列：将target放在外循环，将nums放在内循环，且target外循环正序

非背包问题

LC516：最长回文子序列

**重点：**for循环以下两种都可以，即i在外层或内层都可以，只要确定求当前状态dp[i][j]时之前的状态dp[i+1][j-1]已经求出即可，所以只要确保i是逆序遍历，j是正序遍历，再保证i和j的先后顺序(本题是i<=j)即可

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size()+1, vector<int>(s.size()+1,0));

        //以下两种遍历方式都可
        // for (int i = s.size(); i >= 1; i--) 
        //     for (int j = i; j <= s.size(); j++) 

        for (int j = 1; j <= s.size(); j++) {
            for (int i = j; i >= 1; i--) {
                if (i == j) dp[i][j] = 1;
                else if (s[i-1] == s[j-1]) dp[i][j] = dp[i+1][j-1]+2;
                else dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
            }
        }

        return dp[1][s.size()];
    }
};

其他

方向数组

//坐标轴：X为行，向下增长；Y为列，向右增长
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};

目录

algo

差分数组

lowbit（低位）运算

树状数组

数组离散化(压缩)

快速幂

逆元

组合

隔板法

C(n,m)求解

排序

二分模板

归并排序

快速排序

堆排序

图

Dijkstra

Floyd算法

BFS求图的相关问题

trie树

并查集

LRU

LFU

位运算

方向数组

动态规划

背包问题

非背包问题

其他

方向数组